Automated Verification and Synthesis of Stochastic Cyber-Physical Systems
Automated controller synthesis for complex stochastic systems to achieve some high-level specifications, e.g. those expressed as linear temporal logic (LTL) formulae, is inherently very challenging. To reduce this complexity, one promising approach is to employ (in)finite abstractions of given systems as replacements in the controller synthesis procedure. In this regard, one can first abstract the original (concrete) system by a simpler one (with possibly lower dimension or finite state set), then perform analysis and synthesis over the abstract model, and finally carry the results back (via an interface map) over the concrete system. Since the mismatch between outputs of the original system and that of its abstraction is well-quantified, one can guarantee that the concrete system also satisfies the same specifications as the abstract one with guaranteed error bounds.
The computational complexity in synthesizing controllers for large-scale stochastic systems can be alleviated via abstractions in two consecutive stages. In the first phase, one can abstract the original system by a simpler one with a lower dimension (infinite abstraction). Then one can construct a finite abstraction as an approximate description of the (reduced-order) system in which each discrete state corresponds to a collection of continuous states of the (reduced-order) system. Since the final abstractions are finite, algorithmic machineries from computer science are applicable to synthesize controllers enforcing complex properties over the concrete systems.
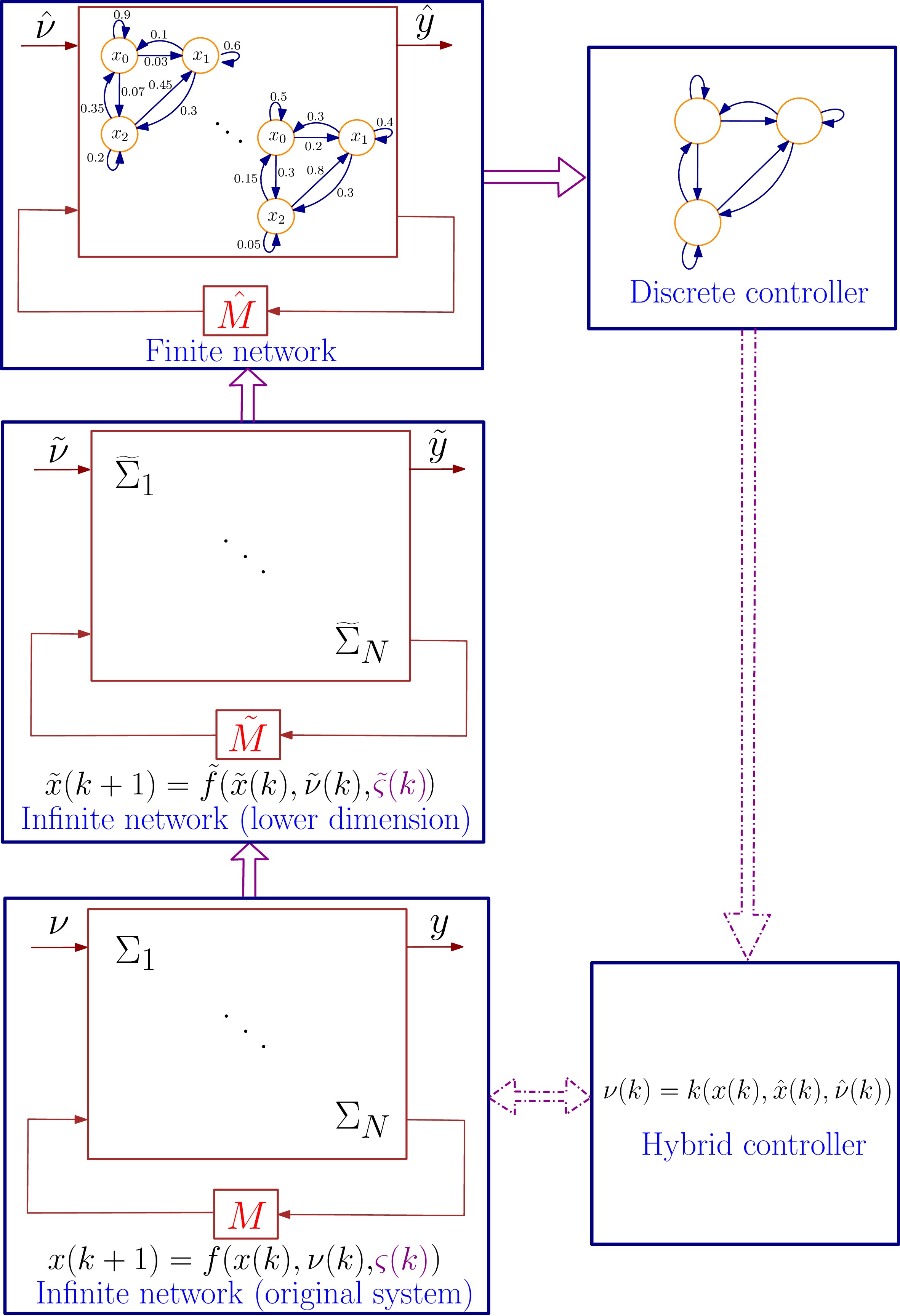
Unfortunately, construction of (in)finite abstractions for large-scale stochastic systems in a monolithic manner suffers severely from the curse of dimensionality. To mitigate this issue, our proposed solution is to consider the large-scale stochastic system as an interconnected system composed of several smaller subsystems, and provide a compositional framework for the construction of (in)finite abstractions for the given system using abstractions of smaller subsystems.
Active Group Members
The following group members are actively working on this topic:
Abolfazl Lavaei
Majid Zamani
Related Publications
The following publications are related to this active topic:
A. Lavaei, S. Soudjani, and M. Zamani, Compositional Abstraction-based Synthesis of General MDPs via Approximate Probabilistic Relations, Submitted for publication, 2019.
A. Lavaei, S. Soudjani, and M. Zamani, Compositional Abstraction-based Synthesis for Networks of Stochastic Switched Systems, Automatica, to appear as a regular paper, 2019.
A. Lavaei, S. Soudjani, and M. Zamani, Compositional (In)Finite Abstractions for Large-Scale Interconnected Stochastic Systems, IEEE Transactions on Automatic Control, conditionally accepted as a full paper, 2019.
A. Lavaei, S. Soudjani, and M. Zamani, Compositional Synthesis of Large-Scale Stochastic Systems: A Relaxed Dissipativity Approach, Nonlinear Analysis: Hybrid Systems, conditionally accepted, 2019.
A. Lavaei, S. Soudjani, and M. Zamani, Compositional Construction of Infinite Abstractions for Networks of Stochastic Control Systems, Automatica, vol. 107, pp. 125-137, 2019.
A. Lavaei, and M. Zamani, Compositional Construction of Finite MDPs for Large-Scale Stochastic Switched Systems: A Dissipativity Approach, 15th IFAC Symposium on Large-Scale Complex Systems: Theory and Applications (LSS), vol. 52, no. 3, pp. 31-36, 2019. (IFAC Young Author Award Finalist)
A. Lavaei, S. Soudjani, and M. Zamani, From Dissipativity Theory to Compositional Construction of Finite Markov Decision Processes, 21st ACM International Conference on Hybrid Systems: Computation and Control (HSCC), pp. 21-30, 2018.
A. Lavaei, S. Soudjani, and M. Zamani, Compositional Synthesis of Finite Abstractions for Continuous-Space Stochastic Control Systems: A Small-Gain Approach, 6th IFAC Conference on Analysis and Design of Hybrid Systems (ADHS), vol. 51, no. 16, pp. 265-270, 2018.
A. Lavaei, S. Soudjani, and M. Zamani, Approximate Probabilistic Relations for Compositional Synthesis of Stochastic Systems, Numerical Software Verification (NSV), Lecture Notes in Computer Science 11652, pp. 101–109, Springer, 2019.
A. Lavaei, and M. Zamani, Compositional Verification of Large-Scale Stochastic Systems via Relaxed Small-Gain Conditions, 58th IEEE Conference on Decision and Control (CDC), to appear, 2019.
A. Lavaei, S. Soudjani, R. Majumdar, and M. Zamani, Compositional Abstractions of Interconnected Discrete-Time Stochastic Control Systems, 56th IEEE Conference on Decision and Control (CDC), pp. 3551-3556, 2017.
A. Lavaei, S. Soudjani, and M. Zamani, Compositional Synthesis of not Necessarily Stabilizable Stochastic Systems via Finite Abstractions, 18th European Control Conference (ECC), pp. 2802–2807, 2019.
A. Lavaei, and M. Zamani, Compositional Finite Abstractions for Large-Scale Stochastic Switched Systems, 5th International Workshop on Symbolic-Numeric Methods for Reasoning about CPS and IoT (SNR) in conjunction with Cyber-Physical Systems and Internet-of-Things Week (CPS-IoT Week), pp. 3-5, 2019.
A. Lavaei, S. Soudjani, and M. Zamani, Compositional Synthesis of Interconnected Stochastic Control Systems based on Finite MDPs, 21st ACM International Conference on Hybrid Systems: Computation and Control (HSCC), pp. 273-274, 2018.